قضیه چهاررنگ




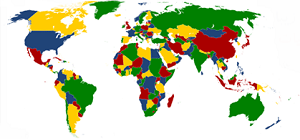
قضیه‌ی چهاررنگ یا حدس چهاررنگ از مسائل مشهور و قدیمی ریاضیات است که سال‌ها اثبات نشده مانده بود. به بیان ساده (و نادقیق) این قضیه می‌گوید:
برای رنگ کردن هر نقشه به طوری که کشورها و نواحی همسایه در نقشه هم‌رنگ نباشند فقط چهار رنگ کافی است.

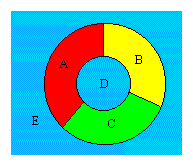
سه رنگ برای نقشه های ساده تر کافیست ولی یک رنگ چهارم اضافی برای برخی نقشه ها لازم است. مثل نقشه هایی که در آن ها یک ناحیه با تعداد فرد نواحی دیگر احاطه شده است که به یکدیگر در یک دایره وصل هستند.


قضیه 5 رنگ که اثباتی کوتاه و ساده دارد، بیان می کند که 5 رنگ برای رنگ آمیزی نقشه کافیست. این قصیه در اواخر قرن ۱۹ اثبات شده است(هیووو ۱۸۹۰).



اثبات اینکه 4 رنگ کافیست بسیار سخت تر است. تعدادی اثبات های غلط و مثال های نقض از زمان ارائه قضیه 4 رنگ در 1852 بیان شده اند. این مسئله به صورت معادله ابتدا درسال 1852 عنوان شد و سرانجام در سال 1976 با کمک رایانه توسط  کی اپل (Appel) و و. هیکن (Haken) حل شد. این اولین قضیه مهمی بود که با استفاده از کامپیوتر به اثبات رسید.

آنها نشان دادند که مجموعه ای از 1936 نقشه وجود دارد که هیچ کدام از آنها نمی توانند قسمتی از یکی از کوچکترین مثال نقض های قضیه چهار رنگ باشند. اپل و هیکن از یک برنامه کامپیوتری خاص منظوره استفاده کردند تا ثابت کنند هیچ کدام از این نقشه ها از این قاعده مستثنا نیستند. علاوه بر این هر نقشه ای فارغ از این که مثال نقض هست یا نه، حتما قسمتی را شامل می شود که شبیه یکی از آن 1936 نقشه می باشد و اثبات این نیاز به صدها صفحه تحلیل دست نویس بود.
اپل و هیکن نتیجه گرفتند که اگر بخواهد کوچکترین مثال نقضی وجود داشته باشد باید شامل یکی از آن 1936 نقشه باشد. این تناقض به این معنی بود که هیچ مثال نقضی وجود ندارد و قضیه درست می باشد. در ابتدا اثبات آنها از طرف همه ریاضیدان ها مورد تایید واقع نشد، چرا که چک کردن یک اثبات کامپیوتری توسط انسان امکان پذیر نبود.

برای اطلاعات بیشتر کلیک کنید.

منبع: ویکی پدیا - سایت رشد