حل رادیکال های مسلسل ساده
حل رادیکال های مسلسل ساده
شاید تاکنون در کتاب های ریاضی عباراتی مانند زیر را دیده باشید:
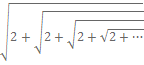
اینگونه رادیکالها را رادیکال های مسلسل (سلسله وار) نامتناهی یا در لاتین Infinite Nested Radicals می نامند. برای محاسبه اینگونه رادیکالها روش های گوناگونی ارائه شده و شاید برای نخستین بار مسائلی از اینگونه در یادداشت های رامانوجان ریاضیدان خودآموخته هندی به طور دقیق مطرح و به کمک اتحاد هایی که بعدها اتحاد های رامانوجان نام گرفت حل گردید. هاردی ریاضیدان انگلیسی در مورد وی گفته است او همردیف ریاضیدان هایی همچون گاوس، اویلر و کوشی بود و باید او را یکی از ریاضیدانان بزرگ دانست. برای محاسبه رادیکال هایی به صورت
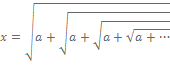
کافی است طرفین رابطه فوق را به توان دو برسانیم در این صورت داریم:
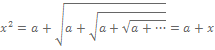
با حل معادله درجه دوم 
خواهیم داشت:
بسته به مقدار 
مقدار 
گنگ یا گویاست. برای اینکه گویا باشد بایستی زیر رادیکال مربع کامل باشد یعنی
بنابراین 
عددی فرد است یعنی: 
.
در نتیجه
بنابراین اگر به صورت حاصلضرب دو عدد متوالی باشد گویا خواهد بود. برای مثال در عبارتی که در بالا ذکر شد داریم:
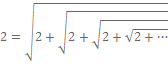
برای اطلاعات بیشتر کلیک کنید.
بر آنیم که ریاضی بیاموزیم اما نه برای ریاضیدان شدن بلکه برای خردمند شدن.